简介

　　我们对数组除了可以进行排序之外，还能对数组中的元素进行查找，其中一个比较经典的方案是利用二分查找法，也叫做折半查找法进行实现，可以缩小查找范围，提高查找效率。

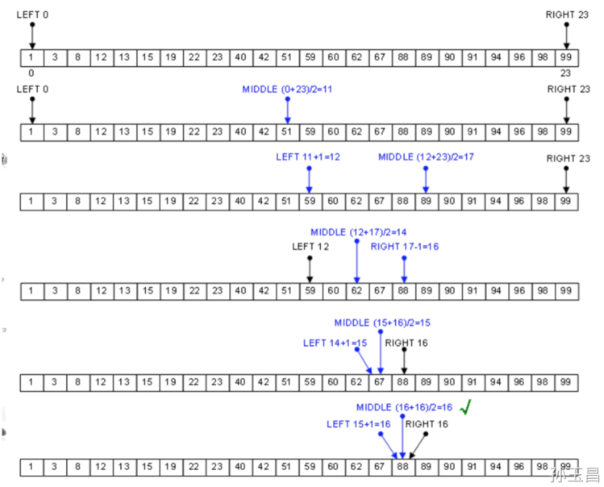
　　二分查找是一种效率较高的查找方法，要求数据表须采用顺序存储结构，且数组是有序(升序或者降序)的。核心思路就是将待查找的元素与中间下标对应的元素进行比较，如果大于中间下标对应的元素，则去右半部分查找，否则就去左半部分进行查找。基本实现流程如下：

　　●首先，我们假设数组中的元素是按升序排列的;

　　●然后将数组中间位置记录的关键字与查找关键字进行比较，如果两者相等，则查找成功;

　　●否则就利用中间的位置记录，将数组分成前、后两个子部分。如果中间位置记录的关键字大于查找关键字，则进一步查找前一子部分，否则进一步查找后一子部分;

　　●重复以上过程，直到找到满足条件的记录为止。或直到子部分不存在为止，此时查找不成功。

　　实现案例

　　然后就按照上述思路，给大家设计了如下案例，大家可以对照练习，好好琢磨该案例。

　　public class Demo14 {

　　public static void main(String[] args) {

　　// 二分查找法--折半查找法

　　// 遍历排序后的数组

　　int[] arr = { 1, 3, 46, 22, 11 };

　　int index = search(arr,46);

　　System.out.println("46所在的索引位置="+index);

　　}

　　//定义一个方法，实现二分查找

　　public static int search(int[] arr,int num) {

　　//1. 获取最小、大值的下标

　　int min = 0;

　　int max = arr.length -1;

　　while(min <= max) {

　　//2. 获取中间值的下标

　　int middle = (min + max) / 2;

　　//3. 将要查找的数字与中间值做比较

　　if(num > arr[middle]) {

　　min = middle +1;

　　}else if(num < arr[middle]) {

　　max = middle -1;

　　}else {

　　return middle;

　　}

　　}

　　return -1;

　　}

　　}

　　3.二分查找法的常见写法

　　1.非递归写法

　　int binarySearch(int[] nums, int target) {

　　int left = 0, right = nums.length - 1;

　　while (left <= right) {

　　int mid = left + (right - left) / 2;

　　if (nums[mid] == target) {

　　return mid;

　　} else if (nums[mid] < target) {

　　left = mid + 1;

　　} else {

　　right = mid - 1;

　　}

　　}

　　return -1;

　　}

　　2.递归写法

　　int binarySearch(int[] nums, int target, int left, int right) {

　　if (left > right) {

　　return -1;

　　}

　　int mid = left + (right - left) / 2;

　　if (nums[mid] == target) {

　　return mid;

　　} else if (nums[mid] < target) {

　　return binarySearch(nums, target, mid + 1, right);

　　} else {

　　return binarySearch(nums, target, left, mid - 1);

　　}

　　}

　　3.查找第一个等于目标值的元素

　　int binarySearch(int[] nums, int target) {

　　int left = 0, right = nums.length - 1;

　　while (left <= right) {

　　int mid = left + (right - left) / 2;

　　if (nums[mid] < target) {

　　left = mid + 1;

　　} else if (nums[mid] > target) {

　　right = mid - 1;

　　} else {

　　if (mid == 0 || nums[mid - 1] != target) {

　　return mid;

　　} else {

　　right = mid - 1;

　　}

　　}

　　}

　　return -1;

　　}

　　4.查找最后一个等于目标值的元素

　　int binarySearch(int[] nums, int target) {

　　int left = 0, right = nums.length - 1;

　　while (left <= right) {

　　int mid = left + (right - left) / 2;

　　if (nums[mid] < target) {

　　left = mid + 1;

　　} else if (nums[mid] > target) {

　　right = mid - 1;

　　} else {

　　if (mid == nums.length - 1 || nums[mid + 1] != target) {

　　return mid;

　　} else {

　　left = mid + 1;

　　}

　　}

　　}

　　return -1;

　　}

　　5.查找第一个大于等于目标值的元素

　　int binarySearch(int[] nums, int target) {

　　int left = 0, right = nums.length - 1;

　　while (left <= right) {

　　int mid = left + (right - left) / 2;

　　if (nums[mid] < target) {

　　left = mid + 1;

　　} else {

　　if (mid == 0 || nums[mid - 1] < target) {

　　return mid;

　　} else {

　　right = mid - 1;

　　}

　　}

　　}

　　return -1;

　　}

　　6.查找最后一个小于等于目标值的元素

　　int binarySearch(int[] nums, int target) {

　　int left = 0, right = nums.length - 1;

　　while (left <= right) {

　　int mid = left + (right - left) / 2;

　　if (nums[mid] > target) {

　　right = mid - 1;

　　} else {

　　if (mid == nums.length - 1 || nums[mid + 1] > target) {

　　return mid;

　　} else {

　　left = mid + 1;

　　}

　　}

　　}

　　return -1;

　　}

　　常见的二分查找法写法的区别

　　1.二分查找有多种写法，主要区别在于查找的目标不同，以及实现方式的不同。非递归写法和递归写法的区别在于实现方式不同，递归写法的代码更加简洁，但是会消耗额外的栈空间。

　　2.查找第一个等于目标值的元素、查找最后一个等于目标值的元素、查找第一个大于等于目标值的元素、查找最后一个小于等于目标值的元素等，主要区别在于对于目标值相等的元素的处理方式不同，需要特别判断。

　　3.另外，二分查找还有一种写法是针对旋转排序数组的，即先找到旋转点，再根据目标值所在的区间进行查找。这种写法和普通的二分查找的区别在于需要先找到旋转点。

　　总的来说，不同的二分查找写法主要针对不同的问题进行了优化，选择哪种写法取决于具体的问题情况。

声明：本站稿件版权均属千锋教育所有，未经许可不得擅自转载。